صلوات

.
لطفاً برای اطلاع از مطالب قبلی به فهرست مطالب ، آرشیو مطالب قبلی و یا صفحات جانبی مراجعه نمائید.
در پایین همین صفحه شماره های 1و2 تا .... وجود دارد که روی هر
شماره کلیک کنید صفحه جدیدی برای مطالعه بگشوده می شود .
مجموع زوایای خارجی چند ضلعی=360 درجه
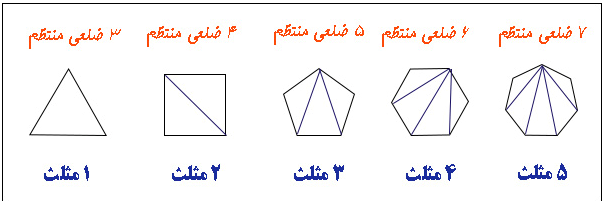
قانون کلی به جدول زیر توجه کنید هر بار یک ضلع به شکلها اضافه میکنیم. 180 درجه به مجموع اضافه میشود
|
نام شکل |
تعدادضلع |
مجموع زاویه های داخلی |
هر یک زاویه |
|
مثلث |
3 |
180° |
60° |
|
4ضلعی |
4 |
360° |
90° |
|
5ضلعی |
5 |
540° |
108° |
|
6ضلعی |
6 |
720° |
120° |
|
7ضلعی |
7 |
900° |
128.57...° |
|
8ضلعی |
8 |
1080° |
135° |
|
... |
... |
... |
... |
|
چند ضلعی |
n |
(n-2) × 180° |
(n-2) × 180° / n |
باتوجه به جدول اگر 2 را از تعداد ضلع n کم کنیم تعداد مثلت داخل چند ضلعی به دست می آید. که تعداد مثلث را در 180 درجه ضرب کنیم .چرا عدد 2 را کم کنیم ؟زیرا با 2ضلع مثلث نمی سازیم .مثال:مجموع زاویه های داخلی یک 10 ضلعی چند درجه است؟ وهریک زاویه چند درجه است؟
اگر پاسخ را از 180 کم کنی یک زاویه خارجی می شود
باتوجه به جدول اگر 2 را از تعداد ضلع n کم کنیم تعداد مثلت داخل چند ضلعی به دست می آید. که تعداد مثلث را در 180 درجه ضرب کنیم .چرا عدد 2 را کم کنیم ؟زیرا با 2ضلع مثلث نمی سازیم .مثال:مجموع زاویه های داخلی یک 10 ضلعی چند درجه است؟ وهریک زاویه چند درجه است؟
(n-2) × 180° = (10-2)×180° = 8×180° = 1440° =
مجموع زاویه ها1440 درجه است. و1440 را بر10 تقسیم می کنیم تا یک زاویه به دست آید.
1440°/10 = 144° که یک زاویه 144 درجه است
ریاضی ششم فصل3
درسنامه فصل سوم (ریاضی کلاس ششم): اعداد اعشاری
1-عددهای اعشاری نمایشی از عددهای کسری یا مخلوط هستند که مخرجشان 10 یا 100 یا … میباشد.
2-برای تبدیل کسر به اعشار دو راه داریم:
الف) مخرج را به 10 یا 100 یا 1000 یا … برسانیم.
ب) صورت را بر مخرج تقسیم میکنیم.
3-برای خواندن عدد اعشاری ابتدا قسمت عدد صحیح را میخوانیم، بعد قسمت اعشاری را میخوانیم و بعد آخرین مرتبه اعشاری را میخوانیم.
مثلاً اگر سه رقم اعشار داشته باشیم، میگوییم هزارم.
4-اگر یکان عدد صحیح صفر بود، بعد از خواندن قسمت عدد صحیح میگوییم: «عدد صحیح و»
مثال: عدد مقابل را بخوانید: 20/05 میخوانیم بیست عدد صحیح و پنج صدم.
5-صفرهای جلوی عدد اعشاری خوانده نمیشود.
6-برای
مقایسه دو عدد اعشاری ابتدا نگاه به عدد صحیح میکنیم اگر برابر بود به
ترتیب به دهم، صدم، … نگاه میکنیم، هر کدام بزرگتر بود آن عدد بزرگتر است.
7-در
جمع و تفریق دو عدد اعشاری باید دقت کرد ممیز زیر ممیز باشد و هر مرتبه
حتماً زیر مرتبه خود نوشته شود و هنگام جمع یا تفریق در جواب به ممیز
میرسیم، ممیز میزنیم.
8-در ضرب اعشار به ممیز توجه نمیکنیم، ضرب را
انجام میدهیم، وقتی پاسخ به دست آمد به تعداد رقمهای اعشاری از سمت راست
میشماریم و ممیز میزنیم.
9-در ضرب و تقسیم بر (10 و 100 و 1000 و …):
الف) در ضرب به تعداد صفرها ممیز به جلو میرود.
ب) در تقسیم به تعداد صفرها ممیز به عقب میرود.
10-در تقسیم اعشاری به ممیز میرسیم ابتدا خط ممیز را ادامه میدهیم و یک ممیز در خارج قسمت میزنیم، بعد تقسیم را ادامه میدهیم.
11-در تقسیم نوع اول یعنی مقسوم علیه عدد صحیح میباشد، تعداد رقمهای اعشاری مقسوم و باقیمانده برابر است.
12-تعداد دور × محیط = مسافت پیموده شده
13-اگر مقسوم و مقسوم علیه تقسیمی را در عددی غیر از صفر ضرب کنیم خارج قسمت تغییر نمیکند ولی باقیمانده در همان عدد ضرب میشود.
14-وقتی
بخواهیم تقسیم نوع دوم (مقسوم علیه اعشاری باشد) را حل کنیم ابتدا آن را
در 10 یا 100 یا … ضرب میکنیم، که بستگی به تعداد رقمهای اعشاری مقسوم علیه
دارد، مثلاً اگر یک رقم اعشار دارد در ده ضرب میکنیم تا ممیز از بین برود و
تقسیم را انجام میدهیم و خارج قسمت را مینویسیم و باقیمانده را بر همان
عدد تقسیم میکنیم.
ریاضی ششم فصل2
درسنامه فصل دوم (ریاضی کلاس ششم): کسر
1-برای جمع یا تفریق کسر ابتدا باید مخرج مشترک بگیریم.
2-برای ساختن کسرهای مساوی: صورت و مخرج را در یک عدد غیر از صفر ضرب میکنیم.
3-راههای مخرج مشترک:
الف) اگر به هم بخشپذیرند مخرج بزرگتر را میگیریم.
ب) اگر به هم بخشپذیر نیستند و به یک عدد مشترک هم بخشپذیر نیستند در هم ضرب میکنیم.
ج) اگر به یک عدد مشترک بخشپذیرند از کوچکترین مضرب مشترک استفاده میکنیم.
4-برای کوچکترین مضرب مشترک:
الف) مضربهای دو عدد را مینویسیم و اولین مضرب مشترک را انتخاب میکنیم.
ب) بزرگترین عامل مشترک بین دو عدد را پیدا کرده و به صورت تساوی ضرب مینویسیم و یک عدد مشترک را خط میزنیم. مثال: بین 36 و 27
108 و81 و54و 27 الف مضربها
144 و108 و72و 36
کوچکترین مضرب مشترک27 و36= 108 =9×4×9× 3
5-ضرب کسر: صورت × صورت میشود صورت مینویسیم و مخرج × مخرج میشود در مخرج مینویسیم.
6-در ضرب کسر قبل از ضرب کردن اگر ساده میشود بهتر است ساده کنیم بعد ضرب کنیم.
7-برای معکوس کردن کسر جای صورت و مخرج را عوض میکنیم.
8-هر گاه حاصل ضرب دو عدد برابر 1 باشد، آن دو عدد را «معکوس» یکدیگر مینامند، همه اعداد به جز صفر معکوس دارند.
9-به طور کلی در تساوی دو کسر مانند ، از رابطه زیر به دست میآید.
10-برای تقسیم دو کسر با مخرجهای برابر کافی است صورتهای آنها را بر یکدیگر تقسیم کنیم.
11-برای تقسیم دو کسر کافی است که کسر اول را در معکوس کسر دوم ضرب کنیم.
12-در کسرهای ترکیبی ابتدا تساویهای صورت و مخرج را حل میکنیم سپس صورت را بر مخرج تقسیم میکنیم.
13-برای مقایسه دو عدد مخلوط ابتدا عددهای صحیح و سپس کسرها را مقایسه میکنیم.
14-برای تقسیم کردن کسر میتوان از دور×دور = صورت، نزدیک × نزدیک = مخرج استفاده کرد.
اعداد زوج وفرد
اعداد صحیح با توجه به بخشپذیریشان به عدد دو، به دو بخش زوج و فرد تقسیم میشوند. اعداد فرد به اعداد صحیحی گفته میشوند که بر دو بخش پذیر نباشند. (حاصل تقسیم آنها به دو نیمه یک عدد صحیح و باقیمانده یک باشد. اعداد فرد در ریاضی در مقابل اعداد زوج قرار دارند و مضرب دو نیستند. یک و منفی سه از اعداد فرد هستند. كه فرمول اعداد فرد میشود 2n-1صفر، چهار و منفی دو از اعداد زوج هستند. به ازای هر عدد صحیح مانند n هر عدد k زوج است اگر و تنها اگر k=۲n باشد یا عدد صحیحی که ۲ را عاد کند زوج است (در حالت کلی تر اگر عددی، عدد زوجی را عاد کند زوج است) به ازای هر عدد صحیح مانند n هر عدد p فرد است اگر و تنها اگر p=۲n-۱ باشد یا عدد صحیحی که ۲ را عاد نکند فرد است (در حالت کلی تر اگر این عدد صحیح هیچ عدد زوجی را عاد نکند فرد است) به عبارت دیگر برای اثبات زوج بودن یک عدد کافی است ثابت کنیم از یک عدد فرد یک واحد کمتر است (یا بیشتر است) به همین صورت برای اثبات فرد بودن یک عدد کافی است ثابت کنیم از یک عدد زوج یک واد بیشتر (یا کمتر) است
- اعداد -۱ و -۳ و … فرد هستند
- اعداد -۲ و -۴ و … زوج هستند
- عدد صفر عددی زوج است
چون که هر عددی را که بر دو تقسیم کنیم و حاصل عددی صحیح باشد زوج محسوب
میشود. عدد صفر از این امتحان سربلند بیرون میآید، چرا که اگر آن را
تقسیم بر دو کنید نتیجه میشود صفر که خود عددی صحیح است.
- حاصل جمع دو عدد زوج، زوج است.
- حاصل جمع دو عدد فرد، زوج است.
- حاصل جمع یک عدد زوج با یک عدد فرد، فرد است
- حاصل ضرب یک عدد فرد در هر عدد فردی، فرد است.
- حاصل ضرب یک عدد زوج در هر عددصحیح، زوج است.
- جمع سه عدد فرد،فرد است.
- جمع دو تا عدد زوج و یک عدد فرد،فرد است.
ریاضی ششم فصل 1
درسنامه فصل اول (ریاضی کلاس ششم) : الگوهای عددی
1-به اعداد … و … و 10 و 8 و 6 و 4 و 2 اعداد زوج یا مضربهای عدد 2 میگویند.
2-به اعداد … و … و 11 و 9 و 7 و 5 و 3 و 1 اعداد فرد میگویند.
3-حاصل جمع دو عدد زوج، عددی زوج است.
حاصل جمع دو عدد فرد، عددی زوج است.
حاصل جمع عددی زوج با عددی فرد عددی فرد است.
4-اگر بخواهیم مضرب عددی را به دست آوریم آن عدد را به ترتیب در (1 و 2 و 3 و …) ضرب میکنیم.
5-برای تشخیص اعداد زوج و فرد باید به رقم یکان آنها توجه کرد اگر یکان آنها (0، 2، 4، 6 و 8) باشد زوج و اگر
(1 و 3 و 5 و 7و 9) باشد فرد است.
6-اگر به مقدار مساوی اضافه شد
شماره ی2 × مقدار اضافه شدن سپس + یا منها میکنیم. تا شکل دو به دست آید
بعد شماره دو را بر میداریم و الگوی خواسته شده را میگذاریم.
7-نفر در صف: اگر عدد وسطی بود × 2 سپس منهای یک، اگر از دو طرف دو عدد دادند دو عدد را با هم جمع میکنیم سپس منهای یک میکنیم.
8-برای
مقایسه دو عدد ابتدا رقمها را میشماریم هر کدام بیشتر بود بزرگتر است اگر
تعداد برابر بود به رقمهای سمت چپ هر عدد نگاه میکنیم. سپس به رقمهای بعدی
نگاه میکنیم.
9-اگر عددی را بر عدد دیگر تقسیم کنیم و باقی مانده صفر شود میگوییم بخشپذیر است.
10-عددی بر 2 بخشپذیر است که رقم یکانش 0، 2، 4، 6 یا 8 باشد.
11-عددی بر 5 بخشپذیر است که رقم یکانش 0 یا 5 باشد.
12-عددی بر 3 بخشپذیر است که جمع رقمهایش بر 3 بخشپذیر باشد و عددی بر 9 بخشپذیر است که جمع رقمهایش بر 9 بخشپذیر باشد.
13-قرینه ی هر عدد با عوض کردن علامت به دست میآید.
14-در مقایسه ی دو عدد منفی: عددی که به صفر نزدیکتر است بزرگتر است یا عددی که ظاهرش بزرگتر است کوچکتر است.
قطر مستطیل
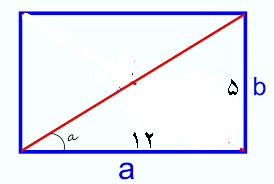
- هر مستطیل دارای دو قطر است که اندازه این قطرها از فرمول زیر محاسبه میشود:(a طول مستطیل وb عرض آن است)
اندازه قطر مستطیل برابر است با مجذورِ مجموعِ مربعِ طول و مربعِ عرض.
(²عرض+²طول)√ = قطر
مثال: مستطیلی با ابعاد 12 سانتیمتر و 5 سانتیمتر داریم. اندازه قطر آن چقدر است؟
√(52 + 122) = √(25 + 144) = √169 = 13 cm
قطر اشکال هندسی یعنی چه

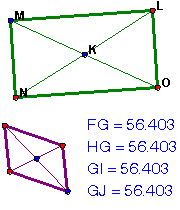
از آنجا که قطر رئوس غیر مجاور را متصل میکند، یک مثلث نمیتواند قطر داشته باشد و یک چهارضلعی (مربع یا مستطیل) دو قطر دارد. تمام قطرهای یک چندضلعی کوژ درون آن هستند، اما چند قطر یک چندضلعی کاو بیرون از آن قرار میگیرد. تعداد قطرهای یک n-ضلعی (n ≥ ۳) کوژ یا کاو از این رابطه بدست میآید:
- یک مربع (یا هر چهارضلعی) دارای 2 = 2 / (3-4) 4 قطر میباشد.
- یک هشت ضلعی دارای 20 = 2 / (3-8) 8 قطر میباشد.
- یک مثلث دارای 0 = 2 / (3-3) 3 قطر میباشد.
در چندضلعیهای مقعر، قطر میتواند از خارج از هندسه نیز عبور کند؛ مثالی از این حالت در شکل زیر نمایش داده شده است.
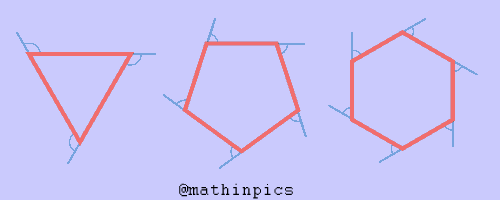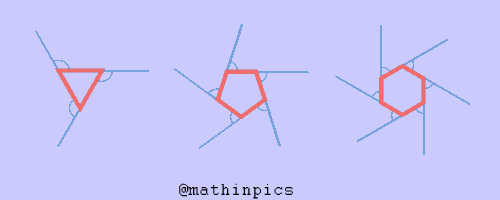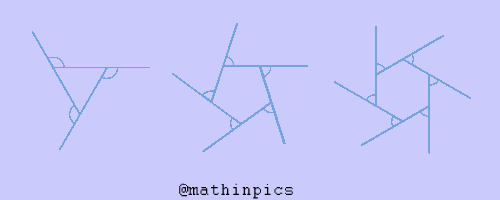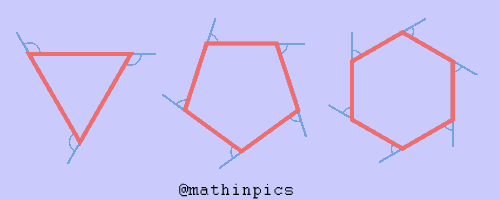
زاویه های داخلی و خارجی چند ضلعی ها
زاویه داخلی
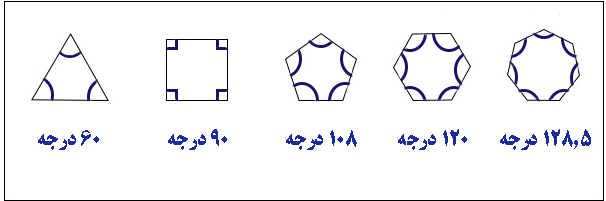
مجموع زاویه های داخلی یک چند ضلعی منتظم چند است؟
اندازه هر زاویه داخلی در چند ضلعی های منتظم
چون در چند ضلعی های منتظم همه زاویه ها با هم مساوی است، پس با تقسیم مجموع زاویه ها بر تعداد آن ها، اندازه هر زاویه داخلی
تعداد اضلاع / ۱۸۰ × ( ۲ – تعداد اضلاع ) = اندازه هر زاویه داخلی در چند ضلعی های منتظم
مجموع زاویه های داخلی 15 ضلعی چند درجه
مجموع زاویه های داخلی ۲۳۴۰=۱۳×۱۸۰ یک پانزده ضلعی
زاویه خارجی
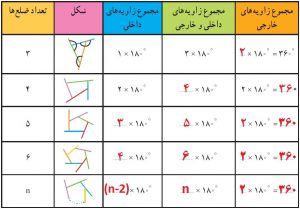
رابطه بین زاویه داخلی و خارجی در هر گوشه
در هر گوشه جمع زاویه داخلی و خارجی مساوی ۱۸۰ است.
محاسبه زاویه های خارجی در چند ضلعی های منتظم
میدانیم از تعداد اضلاع ۲ تا کم کنیم و جوابش را در ۱۸۰ ضرب کنیم، مجموع زاویه های داخلی چند ضلعی منتظم بدست میاید.
میدانیم مجموع زاویه داخلی و خارجی در هر گوشه هم برابر ۱۸۰ میشود. پس مجموع زاویه های داخلی و خارجی کل شکل را اگه بخواهیم باید تعداد گوشه ها را در ۱۸۰ ضرب کنیم
با دانستن این دو مورد ستون سوم و چهارم جدول رو کامل میکنیم. حالا برای پرکردن ستون آخر باید ستون سوم رو از ستون چهارم کم کنیم. اگه دقت کنید این اختلاف همه شکل ها ۳۶۰=۱۸۰×۲ بدست امده. از این تمرین نتیجه میگیریم که :
مجموع زاویه های خارجی همیشه مساوی ۳۶۰ است.
محاسبه هر زاویه خارجی یک چند ضلعی منتظم
در چند ضلعی های منتظم تمام ضلع ها با هم و تمام زاویه های هم با هم مساوی است. این مطلب برای زاویه های خارجی هم صادق است. یعنی تمام زاویه های خارجی هم باهم مساوی هستند. پس برای پیدا کردن اندازه هر زاویه خارجی در یک چند ضلعی منتظم به صورت زیر عمل می کنیم:
اندازه هر زاویه خارجی در چند ضلعی منتظم مساوی ۳۶۰ تقسیم بر تعداد اضلاع
البته میدونیم که تعداد اضلاع و تعداد زاویه ها باهم برابره !
اثبات اینکه چرا مجموع زاویه های خارجی هر nضلعی برابر ۳۶۰ میشود
در ابتدای درس گفتیم که در هر گوشه از یک چندضلعی جمع زاویه داخلی با زاویه خارجی مساوی با ۱۸۰ میشود یک nضلعی دارای nگوشه است بنابراین جمع همه زاویه های داخلی با همه زاویه های خارجی مساوی با n×۱۸۰ هست. از طرفی میدنیم که جمع همه زاویه های داخلی به تنهایی
n×۱۸۰ – (n-2)×۱۸۰ = ۱۸۰×n – n×۱۸۰ + ۲×۱۸۰ = ۱۸۰n – 180n + 360 = 360
تشخیص عدد اول یا مرکب
1. تشخیص عدد اول یا مرکب
2. بعد از اینکه روش غربال رو یاد گرفتیم ، نوبت این است که تشخیص بدهیم این عدد اول هست یا نه .
5. ابتدا راه کاری که توی کتاب درسی هست . اما بعد یه روش خیلی آسان تر یاد میدهیم. پس تا آخر این درس با من همراه باشید.
6. اولین کاری که باید بکنیم این که جذر تقریبی اآن عدد را بگیریم. حالا عدد داده شده رو بر تمام اعداد اول که کوچکتر یا مساوی جذر تقریبی هستند ، تقسیم میکنیم. اگر به هیچ کدم تقسیم نشد، یعنی ان عدد اول هست. تمام شد و رفت !
7. برای جذر تقریبی گرفتن ، لازم است که توان دوم اعداد طبیعی رو بلد باشیم. به جواب توان دوم میگنویند مجذور . مثلا عدد ۱۶ مجذور عدد ۴ و عدد ۲۵ مجذور عدد ۵ هست.
8. ۱²=۱ , ۲²=۴ , ۳²=۹ , ۴²=۱۶ , ۵²=۲۵
9. ۶²=۳۶ , ۷²=۴۹ , ۸²=۶۴ , ۹²=۸۱ , ۱۰²=۱۰۰
10. ۱۱²=۱۲۱ , ۱۲²=۱۴۴ , ۱۳²=۱۶۹ , ۱۴²=۱۹۶ , ۱۵²=۲۲۵ , …
11. مثلا جذر تقریبی عدد ۴۰ رو میخوام الان حساب کنم. میگم ۴۰ بین کدام دو مجذور پشت سرهم قرار میگیره؟ معلومه بین ۳۶ و ۴۹ هست ! این یعنی که جذرش هم بین ۶ و ۷ درمیاید. پس جذر تقریبی عدد ۴۰ میشود ۶ و خرده ای!
12. ۳۶ < 40 < 49 ⇒ √۳۶ < √۴۰ < √۴۹ ⇒ ۶ < √۴۰ < 7 ⇒ √۴۰ ≈ ۶٫
13. حالا مثال بزنیم :
14. مثال : آیا عدد ۱۳۷ اول است یا مرکب ؟
17. خب حالا عدد ۱۳۷ رو باید بر اعداد اول ۲ و ۳ و ۵ و ۷ و ۱۱ تقسیم کنیم. اگه حتی به یکی از این ها بخش پذیر باشد دیگر اول نیست.
18. ۱۳۷ تقسیم بر ۲ : خارج قسمت ۷۸ و باقی مانده ۱ میشود. ⇐ بر ۲ بخش پذیر نیست
19. ۱۳۷ تقسیم بر ۳ : خارج قسمت ۴۵ و باقی مانده ۲ میشود. ⇐ بر ۳ بخش پذیر نیست
20. ۱۳۷ تقسیم بر ۵ : خارج قسمت ۲۷ و باقی مانده ۲ میشود. ⇐ بر ۵ بخش پذیر نیست
21. ۱۳۷ تقسیم بر ۷ : خارج قسمت ۱۹ و باقی مانده ۴ میشود. ⇐ بر ۷ بخش پذیر نیست
22. ۱۳۷ تقسیم بر ۱۱ : خارج قسمت ۱۲ و باقی مانده ۵ میشود. ⇐ بر ۱۱ بخش پذیر نیست
23. چون ۱۳۷ بر هیچ کدوم از اعداد ۲ و ۳ و ۵ و ۷ و ۱۱ بخش پذیر نیست، بنابراین عددی اول است.
24.
25. روش آسان تر، شما لازم نیست جذر بگیرید. از همان اول شروع کنید به تقسیم کردن عدد داده شده بر اعداد اول ۲ و ۳ و ۵ و ۷ و … به ترتیب. فقط حواستان باشد اگه مجذور عدد اول از عدد داده شده بزرگتر شد، دیگر تقسیم بر ان عدد اول و عددهای اول بعد از ان رو لازم نیست بررسی کنیم.
26. مثال : بررسی کنید که آیا ۱۰۷ اول است یا مرکب ؟
27. مجذور ۲ مساوی ۴ است ( ۱۰۷ > 4 ) بررسی بخش پذیری بر ۲ لازم است: (خارج قسمت ۵۳ و باقی مانده ۲ ) ⇐ بخش پذیر نیست
28. مجذور ۳ مساوی ۹ است ( ۱۰۷ > 9 ) بررسی بخش پذیری بر ۳ لازم است: (خارج قسمت ۳۵ و باقی مانده ۲ ) ⇐ بخش پذیر نیست
2. مجذور ۱۱ مساوی ۱۲۱ است ( ۱۰۷ < ۱۲۱ ) بررسی بخش پذیری بر ۷ و اعداد اول بیشتری لازم نیست
3. چون ۱۰۷ بر هیچ کدوم از اعداد ۲ و ۳ و ۵ و ۷ بخش پذیر نیست، بنابراین عددی اول است.
عدداول
2. آخرین عددی که خط میخورد ؟ ⇐ عدد ۴۹
3. عدد ۳۰ چند بار خط میخورد ؟ ⇐ سه بار ، چون ۳۰=۵×۳×۲ یعنی مضرب ۲ و ۳ و ۵ است.
4. خط زدن مضرب های کدام اعداد اول نیاز بود ؟ ⇐ اعداد اول ۲ ، ۳ ، ۵ ، ۷
5. آخرین مضرب ۱۱ که خط میخورد چند است ؟ ⇐ کلا نیازی به خط زدن مضرب های ۱۱ نیست !
6. عدد ۱۵ زودتر خط میخورد یا ۱۶ ؟ ⇐ عدد ۱۶ چون مضرب ۲ است ولی ۱۵ مضرب ۳ . مضرب های ۲ زودتر از مضرب های ۳ خط میخورند.
7. کدام مضرب ۵ است که برای اولین بار در زمان خط زدن مضرب های ۵ خط میخورد و قبلا خط نخورده بوده؟ ⇐ عدد ۲۵
اعداد اول به روش غربال
تعیین اعداد اول به روش غربال چگونه است ؟
مثال : اعداد اول بین ۱ تا ۶۰ را به روش غربال پیدا کنید.
پاسخ : ابتدا اعداد رو از ۱ تا ۶۰ به صورت مرتب مینویسیم. برای تعیین اعداد اول به روش غربال ، طی چند مرحله که الان کامل براتون توضیح میدم شروع میکنیم به خط زدن مضرب های عددهای اول معروف یعنی همون ۲ ، ۳ ، ۵ ، ۷ ، ۱۱ ، ۱۳ ، ۱۷ ، ۱۹ و … که در واقع عددهایی که خط میزنیم اول نیستن و آخر کار هرچی که خط نخورده باقی میمونه عدد اول هست. مراحل کار رو به ترتیب باهم دنبال میکنیم :
۱ ) اول از همه عدد ۱ رو خط میزنیم چون این عدد نه اول هست و نه مرکب. پس همیشه خطش میزنیم. ۱ ۲ ۳ ۴ ۵ ۶ ۷ ۸ ۹ ۱۰
۱۱ ۱۲ ۱۳ ۱۴ ۱۵ ۱۶ ۱۷ ۱۸ ۱۹ ۲۰
۲۱ ۲۲ ۲۳ ۲۴ ۲۵ ۲۶ ۲۷ ۲۸ ۲۹ ۳۰
۳۱ ۳۲ ۳۳ ۳۴ ۳۵ ۳۶ ۳۷ ۳۸ ۳۹ ۴۰
۴۱ ۴۲ ۴۳ ۴۴ ۴۵ ۴۶ ۴۷ ۴۸ ۴۹ ۵۰
۵۱ ۵۲ ۵۳ ۵۴ ۵۵ ۵۶ ۵۷ ۵۸ ۵۹ ۶۰
۲ ) بعد میریم به سراغ خط زدن مضرب های عدد ۲ که در واقع همون اعداد زوج هستن. هرچی عدد زوج داریم خط میزنیم. یادتون باشه که خود عدد ۲ رو خط نزنید ها ! اون یه عدد اول خودش.
۱ ۲ ۳ ۴ ۵ ۶ ۷ ۸ ۹ ۱۰
۱۱ ۱۲ ۱۳ ۱۴ ۱۵ ۱۶ ۱۷ ۱۸ ۱۹ ۲۰
۲۱ ۲۲ ۲۳ ۲۴ ۲۵ ۲۶ ۲۷ ۲۸ ۲۹ ۳۰
۳۱ ۳۲ ۳۳ ۳۴ ۳۵ ۳۶ ۳۷ ۳۸ ۳۹ ۴۰
۴۱ ۴۲ ۴۳ ۴۴ ۴۵ ۴۶ ۴۷ ۴۸ ۴۹ ۵۰
۵۱ ۵۲ ۵۳ ۵۴ ۵۵ ۵۶ ۵۷ ۵۸ ۵۹ ۶۰
۳ ) بریم سراغ مضرب های عدد ۳ که الان باید خط بخورند ، البته همه بجز خود عدد ۳ ، چون ۳ یک عدد اول هست. همه اعدادی که مجموع رقم ها بر ۳ بخش پذیر هست رو خط میزنم . چون شرط بخش پذیری بر ۳ ،که مجموع رقم های عدد بر ۳ بخش پذیر باشد. هر عددی که بر ۳ بخش پذیر باشدیعنی اینکه مضرب ۳ هستد.
۱۱
۳۱
۴۱
۱۱
۳۱
۴۱
۵ ) موضوعی هست که ما تا کی باید این خط زدن ها رو ادامه بدیم ؟؟؟ قطعا اینطوری نیست که تا هرجا دلمان خواست خط بزنیم، هر وقت خسته شدیم دیگه خط نزنیم. یه راهکاری دارد. اگریه عدد اول رو در خودش ضرب کردیم و دیدیم که جواب از آخرین عدد کوچکتر است، یعنی مضرب های ان عدد اول راباید خط بزنیم. اگر هم که حاصلضرب عدد اول در خودش بیشتر از عدد آخری شد یعنی کار غربال کردن تمام شده و هرچه عدد خط نخورده داریم عدد اول هستش.
واسه این مثال که داشتیم حل میکردیم :
۲ × ۲ = ۴ < 60 ⇒ مضرب های ۲ باید خط بخورند
۳ × ۳ = ۹ < 60 ⇒ مضرب های ۳ باید خط بخورند
۵ × ۵ = ۲۵ < 60 ⇒ مضرب های ۵ باید خط بخورند
۷ × ۷ = ۴۹ < 60 ⇒ مضرب های ۷ باید خط بخورند
۱۱ × ۱۱ = ۱۲۱ > 60 ⇒ نیاز به خط زدن مضرب های ۱۱ نیست و کار غربال تمام است
پس لازمه که مضرب های ۷ راهم خط برنیم. از ۷ شروع به شمردن میکنیم، هفت تا هفت تا جلو میریوم و خط میزنیم. اگه قبلا خط خورده بود اشکالی پیش نمیاید.
۱۱
۳۱
۴۱
اعدادی که خط نخورده باقی مونده رو به رنگ ابی نشان دادیم. ۲ ، ۳ ، ۵ ، ۷ ، ۱۱ ، ۱۳ ، ۱۷ ، ۱۹ ، ۲۳ ، ۲۹ ، ۳۱ ، ۳۷ ، ۴۱ ، ۴۳ ، ۴۷ ، ۵۳ ، ۵۹ اعداد اول هستند
تعداد صفحه تقارن در مکعب
اعداد متداخل ومتباین ومتوافق از1تا 10
رابطه بین اعداد
از نظر محاسبات ارث ، دو عدد یا متساوی و متماثل هستند و یا اینکه مختلف هستند و دو عدد مختلف یا متداخل هستند و یا متوافقند و یا متباین هستند .
فرض تماثل و تساوی که واضح است مثل 2 و 2 .
در صورتی که عدد بزرگتر مضربی از عدد کوچکتر باشد دو عدد متداخل هستند مثل 4و12 ، 3و9 .
و در صورتی که دو عدد مضرب مشترکی غیر از عدد یک داشته باشند آن دو عدد متوافق هستند مثل 10و8 ، 6و9 .
و در غیر این صورت عددها متباین خواهند بود مثل 5و7 ، 3و10 .
نکته : در صورتی که دو عدد دارای مضربهای مشترک متعددی هستند مضرب بزرگتر را ملاک قرار می دهیم مثل 12 و 18 که دارای مضرب مشترک 2 ، 3 و 6 هستند و ملاک محاسبات عدد 6 می باشد .
منبع:سایت دکتراکبراحمدی
1,11,21,1211,111221
اولی یک
دومی ۱۱ هست، یعنی دو تا دونه ۱ که می شود 21
چهارمی ۱۲۱۱ هست یعنی یکی یک، یکی دو، دوتا یک که می شود ۱۱۱۲۲۱
پنجمی ۱۱۱۲۲۱ هست، یعنی ۳ تا یک، دوتا دو، یکی یک یعنی می شود ۳۱۲۲۱۱
پس جواب مسئله ۳۱۲۲۱۱ هست :)
وند ها
وند از نظر جای آن نسبت به پایه بر سه گونه است:
پیشوند، پسوند، میانوند.
پیشوند آنست كه در آغاز پایه میآید: همسفر، نادرست، بیهوش.
پسوند آنست كه در پایان پایه میآید :گلزار، دردمند.
میانوند آنست كه به درون پایه افزوده میگردد: سرتاپا، رنگوارنگ
مهمترین_وند_ها
پر کاربرد ترین پیشوند ها:
با ( با هنر ) – بی ( بی عقل ) – باز ( بازپرس ) – هم ( همراه ) – بر ( بر گشت ) – نا ( نا سپاس ) – نَ (نَسوز )
پر کاربردترین پسوند ها:
بان ( دروازه بان) – دان ( قلم دان) – ستان ( بیمارستان ) – سار ( چشمه سار ) – زار ( لاله زار ) – گر ( کوزه گر) – گری ( یاغی گری) – گاه ( آزمایش گاه) - ــِـ ش ( دانش ) – وار ( امیدوار، دیوانه وار) – چه ( کتابچه) – گین ( اندوهگین) – ناک ( سوزناک) – مند ( اندیش مند) – گار ( آموزگار) - ــَــنده ( دونده) – ان (به غیر از نشانه جمع مثلا گریان، کوهان) – انه ( روزانه) – ار ( دیدار) – ا ( بینا و شنوا) - ه ( نوشته ، هفته ) – ی ( به غیر از ی نکره ، مثلا آهنی ) – ور ( هنرور) - ــــَک ( عروسک)
میانوندها:
این میانوند در ترکیب با واژهای دیگر گاه بر معنای «ترتیب» و گاه بر معنای «همگی» دلالت میکند وپیوسته با واژه ی قبل و بعد خود نوشته میشود:
تنگاتنگ دمادم دوشادوش
رویاروی سراپا سراسر
به
این میانوند برای نشان دادن ترتیب به کار می رود وهمواره با یک فاصله از واژه ی قبل وبعد خود نوشته می شود:
جابه جا رخ به رخ رو به رو زبان به زبان
سینه به سینه لنگه به لنگه مو به مو یک به یک
تا
این میانوند در ترکیب با واژه ای بر معنای همگی وکلی دلالت می کند و همواره با یک فاصله از واژه ی قبل وبعد خود نوشته می شود:
سر تا پا سر تاسر گوش تا گوش
و
این میانوند برای ترکیب دو واژه که با هم بر یک معنای مشترک دلالت میکنند به کار میرود و همواره با یک فاصله از واژه ی قبل و بعد خود نوشته میشود:
شست وشو پرس وجو جست وجو
رُفت وروب کندوکاو گفت وگو



